What denominator does the Cohen's d use on JASP??

biva

As I'm getting different results when calculating Cohen's d with SD Pooled as the denominator to the results JASP is giving me.
I just want to make sure I'm reporting it correctly in my write up.

Cheers,

EJ

I'll ask Johnny what's up. I think the issue came up before. Do you have a concrete example?
Cheers,
E.J.

biva

Here's a couple of examples with the JASP d and the SD Pooled d (calculated using Lee Becker's website):
M1 = 66.5 ± 72.8 M2 = 36.5 ± 30.7 JASP d = 0.84 SD Pooled d = 0.54

M1 = 10.3 ± 14.8 M2 = 2.3 ± 4.1 JASP d = 0.54 SD Pooled d = 0.73

As you can see, they're coming up with vastly different results, both increasing and decreasing the ES, some even changing thresholds (from moderate to large for example).

Cheers

JohnnyB

Hi Biva,
I just ran some examples through both JASP and Lee Becker's calculator, and it seems that they provide the same output whenever the sample sizes in both groups are equal. If the sample sizes between groups differ, they indeed provide different results.
JASP calculates Cohen's d with the following R-code:

num <- (ns[1] - 1) * sds[1]^2 + (ns[2] - 1) * sds[2]^2
sdPooled <- sqrt(num / (ns[1] + ns[2] - 2))
d <- as.numeric((ms[1] - ms[2]) / sdPooled) 

Whereas Lee Becker does the following:

sdPooled <- sqrt((sds[1]^2 + sds[2]^2)/2)
d <- as.numeric((ms[1] - ms[2]) / sdPooled) 

So the latter does not weigh the standard deviations by sample size to determine the pooled standard deviation. My guess would be that Lee Becker's calculator rests on the assumption that the sample sizes are equal.
See also here:
https://en.wikipedia.org/wiki/Effect_size#Cohen.27s_d
http://stackoverflow.com/questions/15436702/estimate-cohens-d-for-effect-size
Andy Field - Discovering Statistics using SPSS

Cheers,
Johnny

biva

Hi, thanks for the reply Johnny.
It makes sense everything you've said, but my sample sizes are equal. I double checked to see if I'd missed any participants from the data set, but they're all there.

Would it be possible to send you a Jasp file with the data set via Dropbox or something?

biva

I've also just ran the following through a couple of other online calculators and they all agree with the 0.54 result:
M1 = 66.5 ± 72.8 M2 = 36.5 ± 30.7 JASP d = 0.84 SD Pooled d = 0.54

I obviously don't want to report incorrect results, and I'm getting concerned about the rest of my results as well at the minute.

EJ

Hi Biva,

Yes, please send us your data set. You can just Email it to EJ.Wagenmakers@gmail.com and I'll forward it to Johnny.

E.J.

biva

Hi,
that's great, I've sent them from C Kirk

Cheers

JohnnyB

Hi Biva,
Thanks again for your help! I took a look at the JASP files you sent us. I was under the impression that you were conducting two-sample t-tests, as you reported the means and sd's for both groups. However, in the JASP files I saw that you are conducting paired samples t-tests.
This has repercussions for the way Cohen's d is calculated. For two-sample t-tests, the formula's I described previously are used, but for paired sample tests, the following formula/code is used:

d <- mean(c1 - c2) / sd(c1 - c2)

where c1 and c2 refer to the scores of the first sample and second sample respectively, so now the denominator is the standard deviation of the difference scores (instead of the pooled standard deviation). One can also compute Cohen's d from the paired samples t-statistic:

d <- t / sqrt(n)

For instance, for your test on the variables WinSigStrLanded and LossSigStrLanded, the paired samples t-statistic equals 4.443, with n = 28. Now, 4.443/sqrt(28) = 0.84.
See also:
https://stats.stackexchange.com/questions/201629/cohens-d-for-dependent-sample-t-test
http://mandeblog.blogspot.nl/2011/05/cohens-d-and-effect-size.html
https://en.wikipedia.org/wiki/Effect_size#Cohen.27s_d (the first part of that section is about Cohen's d for two-sample t-tests, and the second part about Cohen's d for paired samples t-tests)
Please let me know if you have any additional questions, I'd be happy to help!
Cheers,
Johnny

biva

Ah that explains a lot! That's really helpful, thankyou!

Further proof - as if it was needed - that I have a lot more reading and learning to do as well!

Thanks again!

JohnnyB

Hi Biva,
Happy to help, I'm glad that it got sorted out!
Cheers,
Johnny

Karlos

Hi,

Sorry for opening again this discussion, but I wonder why JASP team decided to compute Cohen's d for paired samples the way JohnnyB described, with the standard deviation of the difference scores (SD_diff) as denominator. Cummings (2012) argued against that and Dunlap, Cortina, Vaslow and Burke (1996; Psychological Methods) showed that computing d from the t statistic largely overestimates the effect size because it does not account for the correlation between samples.

I just tried with the data attached (separator is ";").

• In JASP, paired samples t-test shows Cohens d = 0.780, t = 2.466, and r = 0.962.
• Following the formula in Table 1 of Dunlap et al. (1996), d = t[2(1 - r)/n] (note the correlation in the formula), we get d = 2.466* sqrt(2* (1-0.962)/10) = 0.215
• If Cohen's d is computed following Cumming (2012, formula 11.10) and using SDPooled as denominator as JohnnyB posted above (either formula, because n is always the same for paired samples):
  sdPooled <- sqrt((sds[1]^2 + sds[2]^2)/2)
  you get d = (mean1 - mean2) / sdPooled = 5.2 / 21.90 = 0.237.

If you correct d = 0.237 for bias and get Hedge's g, then you get d_unbiased = 0.217, very similar to the outcome with the formula of Dunlap et al. (I may have lost some decimals here and there). In any case, d is more similar using sdPooled and the Dunlap et al. (1996) formula than with JASP and SD_diff.

In general, it seems to me that sdPooled may be a better denominator than SD_diff for paired samples, but I wonder what's the opinion of the JASP team in this matter.

Cheers,

Karlos

cscmac

Comparing two, small different sized groups the Independent Samples T-Test returns an effect size, Cohen's d =-0.916. Putting the same data into the effect size calculator gives a different answer, Cohen's d = 0.944853. This would suggest that the T-Test is returning the value for Hedges' g and not the advertised Cohen's d.
With the same data it is possible to run an Independent ANOVA. The post-hoc test gives a Cohen's d of -0.453. There is a note that Cohen's d does not correct for multiple comparisons but here there is just the one comparison so why the different score?
(I apologise in advance if I am just showing my ignorance of basic statistics and effect sizes.)

JohnnyB

Hi Cscmac,
Interestingly enough there are multiple ways of calculating cohen's d. The difference lies in how the standard deviations are pooled. In JASP we have chosen to use the same method as applied by the effsize package in R:

library(effsize)
dat <- read.csv("/home/johnny/Downloads/vbpggdw47ucs.csv")
cohen.d(dat$time..s. ~ dat$sport, hedges.correction = FALSE) # gives -0.9157262
cohen.d(dat$time..s. ~ dat$sport, hedges.correction = TRUE)  # gives -0.8790971
        #   This is the relevant JASP code, where n1 is sample size, sd1 is standard deviation, and m1 the mean of group 1:
num <-  (n1 - 1) * sd1^2 + (n2 - 1) * sd2^2
sdPooled <- sqrt(num / (n1 + n2 - 2))
if(test==2){ # Use different SE when using Welch T test
  sdPooled <- sqrt(((sd1^2)+(sd2^2))/2)
}
d <- (m1 - m2) / sdPooled # Cohen's d

As you can see, the standard deviations are treated differently, based on whether the Welch t-test is used or not. If you go to JASP and tick the Welch test, you can see that the resulting effect size matches the one you found with the online calculator.
As for the discrepancy with the ANOVA post-hoc test - this was a bug and it has been fixed in a later release of JASP.
Kind regards,
Johnny

pkleka

I have one more question in this topic: how is calculated effect size in case Mann-Whitney test use? d for Student and Welch are only slighty different (and thanks Johnny's explanations I know why), but for M-W it is about 30-40% less. On which statistic it is calculated?

JohnnyB

Hi,
If you look at the table when you only select MW (or, if i remember correctly, look at the footnote of the joint table), it will mention which effect size metric. I think it's the rank biserial correlation. Please let me know if this already clarifies it - Im away from my laptop for a couple of days, so I can be more elaborate when i get back, if needed
Kind regards
Johnny

FSella

Hi Johnny,

could you help me out here?
I have a discrepancy between JASP and cohen.d function (package effsize) in R.
The sleep data set is used as example.

JASP

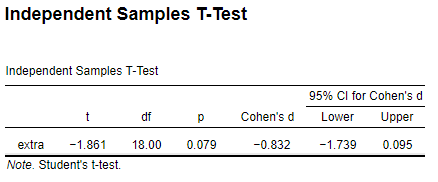
R
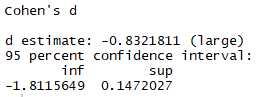
effsize::cohen.d(sleep$extra ~ sleep$group, paired = F, hedges.correction = FALSE)

Same d but different CIs.

Many thanks

Francesco

JohnnyB

Hi Francesco,
Thanks for reporting it, it seems that eff.size package has a new version that has a slightly different algorithm from the previous one - I will update the JASP code accordingly so the next version will have the same output again!
Kind regards,
Johnny

JohnnyB

In addition I looked into this discrepancy a bit more, and there just seem to be multiple ways of computing the confidence intervals for cohen's d (differing in their approximations). There's an interesting post and simulation study here.
Basically, the MBESS package (which is the same as the JASP output) uses a more exact approach and comes out with the best coverage of the true effect size. If you specify the non-central argument in the cohen.d function, you get the same result as JASP/MBESS (paper on MBESS is found here and another illuminating article on the non-centrality parameter and why the MBESS approach is better can be found here).

Kind regards,
Johnny

FSella

Hi Johnny,

in the last version of effsize package, the noncentral option works.
It did not before, as reported in the post you suggested.

When the noncentral option is set = TRUE, the results from JASP and R are the same.
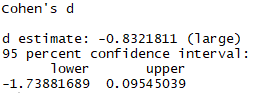
effsize::cohen.d(sleep$extra ~ sleep$group, paired = F, hedges.correction = FALSE, noncentral=T)

Best wishes

Francesco

Chuan-Peng Hu

Hi, Johnny,

This post is really interesting and relevant to my question about the Cohen's d of paired t-test in JASP. If I understand correctly, JASP used the mean and sd of difference between M1 (data from condition 1 fro a within-subject design) and M2 (data from condition 2 fro a within-subject design) when calculating Cohens'd. Also, JASP use the same algorithm as effsize::cohen.d . Based on my understanding, I have a few questions:

(1) Only use mean and sd of difference didn't consider the correlation between M1 and M2, which had been pointed out by others: https://github.com/jasp-stats/jasp-issues/issues/38

(2) Seem that JASP's results is different from effsize::cohen.d in my case. (JASP version 0.11, effsize version 0.7.6). For the data I used, JASP gives Cohen's d = 0.0095, while effsize::cohen.d gives 0.0050383 (paired = T or F gave the same value). I also used the formulas from Cooper, Hedges, & Valentine (2009, The handbook of research synthesis and meta-analysis, see below), the results is similar to the output of effsize::cohen.d .

(3), The 95% CI. Seems that different methods returned different output:

`test.df <- read.csv('df4a.meta_d_w.csv')

## Mothed 0: JASP

# Cohen's d = 0.0095, 95% CI [-0.2457 0.2646]

## Method 1: using effsize and MBESS

d.stat <- effsize::cohen.d(test.df$Other_Neutral, test.df$Other_Bad, conf.level = 0.95,

                          paired=T, hedges.correction = FALSE)$estimate

# output: 0.0050383

MBESS::ci.smd(smd = d.stat, n.1 = 59, n.2 = 59, conf.level = 0.95)

# gives 95% CI [-0.35583 0.36589]

## Method 2: Using t.test and compute.es

t.stat <- t.test(test.df$Other_Neutral, test.df$Other_Bad, paired = T)$statistic

compute.es::tes(t.stat, n.1 = 59, n.2 = 59, level = 95)

# gives cohen's d = 0.01, 95% CI of d [-0.35 0.38]

## Method 3: using formula from Cooper et al., 2009

d.sgpp <- function(m.1,m.2,sd.1,sd.2,n,r=.5)

{

       # m.1 = mean at time 1

       # m.2 = mean at time 2

       # sd.1 = standard dev. at time 1

       # sd.2 = standard dev. at time 2

       # n = sample size

       # r = correlation between time 1 and 2

       s.within <- (sqrt((sd.1^2 + sd.2^2)-2*r*sd.1*sd.2))/(sqrt(2*(1-r)))

       d <- ((m.1 - m.2)/s.within)

       var.d <- 2*(1-r) * (1/n + d^2/(2*n))

       out <- cbind(d, var.d)

       return(out)

}

M1 <- mean(test.df$Other_Neutral)

M2 <- mean(test.df$Other_Bad)

SD1 <- sd(test.df$Other_Neutral)

SD2 <- sd(test.df$Other_Bad)

r_m1_m2 <- cor(test.df$Other_Neutral, test.df$Other_Bad)

# calculate the d and var.d:

coopers_d <- d.sgpp(M1, M2, SD1, SD2, length(test.df$Other_Neutral),r_m1_m2)

# gives d = 0.0050383, var.d = 0.0047705

# Boundaries of CI

lower_CI_coopers <- coopers_d[1] - 1.96 * sqrt(coopers_d[1])   # -0.13408

higher_CI_coopers <- coopers_d[1] + 1.96 * sqrt(coopers_d[1])  # 0.14416

# gives 95% CI [-0.13408 0.14416] `

df4a.meta_d_w.jasp

df4a.meta_d_w.csv

Chuan-Peng Hu

Hi, Johnny,

This post is really interesting and relevant to my question about the Cohen's d of paired t-test in JASP. If I understand correctly, JASP used the mean and sd of difference between M1 (data from condition 1 fro a within-subject design) and M2 (data from condition 2 fro a within-subject design) when calculating Cohens'd. Also, JASP use the same algorithm as effsize::cohen.d . Based on my understanding, I have a few questions:

(1) Only use mean and sd of difference didn't consider the correlation between M1 and M2, which had been pointed out by others: https://github.com/jasp-stats/jasp-issues/issues/38

(2) Seem that JASP's results is different from effsize::cohen.d in my case. (JASP version 0.11, effsize version 0.7.6). For the data I used, JASP gives Cohen's d = 0.0095, while effsize::cohen.d gives 0.0050383 (paired = T or F gave the same value). I also used the formulas from Cooper, Hedges, & Valentine (2009, The handbook of research synthesis and meta-analysis, see below), the results is similar to the output of effsize::cohen.d .

(3), The 95% CI. Seems that different methods returned different output. See my scripts below:

test.df <- read.csv('df4a.meta_d_w.csv')

## Mothed 0: JASP

# Cohen's d = 0.0095, 95% CI [-0.2457 0.2646]

## Method 1: using effsize and MBESS

d.stat <- effsize::cohen.d(test.df$Other_Neutral, test.df$Other_Bad, conf.level = 0.95,

                          paired=T, hedges.correction = FALSE)$estimate

# output: 0.0050383

MBESS::ci.smd(smd = d.stat, n.1 = 59, n.2 = 59, conf.level = 0.95)

# gives 95% CI [-0.35583 0.36589]

## Method 2: Using t.test and compute.es

t.stat <- t.test(test.df$Other_Neutral, test.df$Other_Bad, paired = T)$statistic

compute.es::tes(t.stat, n.1 = 59, n.2 = 59, level = 95)

# gives cohen's d = 0.01, 95% CI of d [-0.35 0.38]

## Method 3: using formula from Cooper et al., 2009

d.sgpp <- function(m.1,m.2,sd.1,sd.2,n,r=.5)

{

       # m.1 = mean at time 1

       # m.2 = mean at time 2

       # sd.1 = standard dev. at time 1

       # sd.2 = standard dev. at time 2

       # n = sample size

       # r = correlation between time 1 and 2

       s.within <- (sqrt((sd.1^2 + sd.2^2)-2*r*sd.1*sd.2))/(sqrt(2*(1-r)))

       d <- ((m.1 - m.2)/s.within)

       var.d <- 2*(1-r) * (1/n + d^2/(2*n))

       out <- cbind(d, var.d)

       return(out)

}

M1 <- mean(test.df$Other_Neutral)

M2 <- mean(test.df$Other_Bad)

SD1 <- sd(test.df$Other_Neutral)

SD2 <- sd(test.df$Other_Bad)

r_m1_m2 <- cor(test.df$Other_Neutral, test.df$Other_Bad)

# calculate the d and var.d:

coopers_d <- d.sgpp(M1, M2, SD1, SD2, length(test.df$Other_Neutral),r_m1_m2)

# gives d = 0.0050383, var.d = 0.0047705

# Boundaries of CI

lower_CI_coopers <- coopers_d[1] - 1.96 * sqrt(coopers_d[1])   # -0.13408

higher_CI_coopers <- coopers_d[1] + 1.96 * sqrt(coopers_d[1])  # 0.14416

# gives 95% CI [-0.13408 0.14416] `

df4a.meta_d_w.jasp

df4a.meta_d_w.csv

JohnnyB

Hi,

Apologies for the late reply, and thanks for your insightful post.

You are right that we use the MBESS package for computing the confidence intervals around the effect sizes. We do this as follows:

unlist(conf.limits.nct(ncp = -0.072947, 59)[c(1,3)]) / sqrt(59)

where the ncp is the observed t-statistic from the paired t-test. This gives the CI for t, and we then divide by sqrt(59) to bring it to the level of the effect size.

I think what goes wrong in your code above (except for Cooper) is that these commands are for the two-sample versions of the effect size, then if you start out with the wrong version of the effect size, this will lead to difference CI bounds.

We compute the effect size as follows for the paired test:

           d  <- mean(c1 - c2) / sd(c1 - c2)

Which indeed does not take into account the correlation between the scores. We are currently working on adding more effect sizes (see two-sample t-test) that do take such matters into account. The Cooper approach looks very appealing also!

Please let me know if anything is still unclear.

Johnny

Chuan-Peng Hu

Dear Johnny,

Thanks for your reply!

I think what goes wrong in your code above (except for Cooper) is that these commands are for the two-sample versions of the effect size

I thought include this argument "paired = T" will render the t-test to paired t-test. Here the t.test function says:

paired: a logical indicating whether you want a paired t-test.

I am still a bit confused ?

Best,

Chuan-Peng