Interpretation of ANOVA interactions

noemielteto

Hi All,

I am an ambitious beginner in Bayesian Statistics and JASP My question regards the computations between the interactions in ANOVA. I would use an example here, where we assess the effect of age and gender on Counting Span test scores. The results should be that there is an effect of age group (kids vs adolescents vs adults), no effect of gender and no effect of gender X age group (based on literature and classical analysis of this data).

As I understand, the main effect BFs in the ANOVA reflect how well the group contrasts support the H1. We have evidence for the effect of age group (high average contrasts among 1 vs 2, 2 vs 3, 1 vs 3 age groups) and evidence for the lack of the effect of gender (low contrast between boys and girls). Is this correct?

Do the interaction effect BF-s reflect contrasts among 2 x 3 = 6 subgroups? If so, how do we treat the
1) same-gender subgroup contrasts
2) same-agegroup subgroup contrasts
3) different gender and different age group subgroup contrasts
differently from each other?

What does explain that we get high BF_10 for the interaction effect, although there should not be one?

Thank you in advance!

Noémi Éltető

sebastiaan

Hi Noémi,

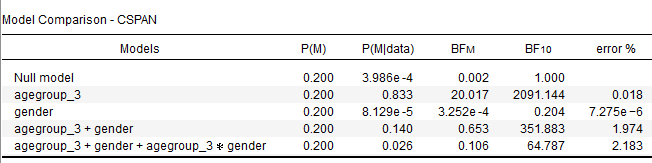
The Bayesian results show exactly what you expect: An effect of age, but no effect gender, nor a gender × age interaction. Why? Well, let's take a look at the table.

For each model, the BF10 reflects the likelihood ratio of the data given the model and the null model. If we look at the age + gender + age × gender model, you see that it does very well compared to the null: BF10 = 64.787. However, the age + gender model (without the interaction) does even better compared to the null: BF10 = 351.883.

So is there any evidence for the interaction? No, because the interaction makes the model worse. How much worse? Well, we can simply divide the BF10 of the model with the interaction by the BF10 of the model without the interaction: BF(age × gender) = 64.787 / 351.883 = 0.18, or substantial evidence against the interaction.

Does that make sense? The Bayes Factors in the table are not for specific effects. They are for models, which can include multiple effects. And to isolate the evidence for a specific effect, you need to compare the models to each other.

Cheers!
Sebastiaan

noemielteto

Hi Sebastiaan,

This was absolutely enlightning. Thank you!

Cheers,
Noémi